No início do século 20, um enigma fascinante da natureza começou a ser desvendado por meio de números e equações. Alfred Lotka, matemático polonês-americano, e Vito Volterra, matemático italiano, trabalharam de forma independente para desenvolver um modelo matemático que descreve a dinâmica entre predadores e presas. Suas contribuições deram origem às equações de Lotka-Volterra, que explicam o comportamento cíclico das populações em relações ecológicas intrínsecas.
A dinâmica entre presas e predadores
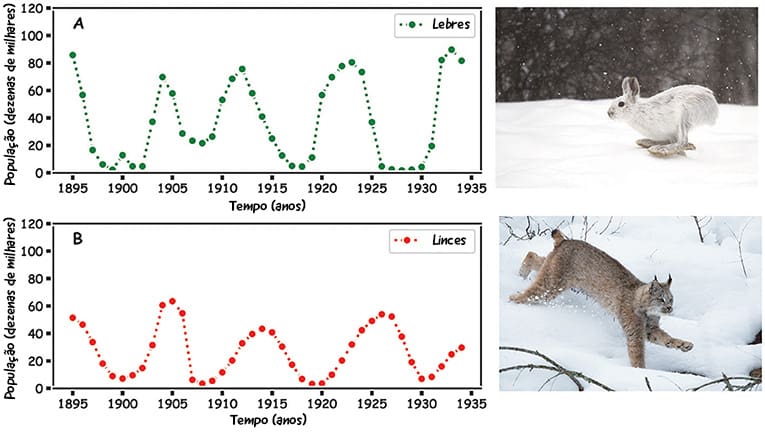
Imagine um ecossistema marinho onde focas e tubarões coexistem. Quando a população de focas aumenta, os tubarões têm à disposição um banquete abundante, permitindo que sua população também cresça. Contudo, o aumento de tubarões eventualmente reduz o número de focas, levando a uma escassez de alimento e à consequente diminuição da população de tubarões. Esse ciclo de abundância e escassez continua indefinidamente, como uma “dança” ecológica previsível pelas equações de Lotka-Volterra.
As equações de Lotka-Volterra consistem em dois componentes principais:
- Equação das presas: Representa o crescimento populacional das presas, considerando sua taxa de reprodução e a pressão exercida pelos predadores.
- Equação dos predadores: Descreve a população dos predadores, que depende diretamente da disponibilidade de presas para sua sobrevivência.
Apesar de simples, essas equações revelam padrões complexos e repetitivos observados na natureza.
A origem do modelo e suas implicações

Alfred Lotka inicialmente aplicou seu modelo ao estudo de reações químicas, mas logo percebeu que os mesmos princípios poderiam ser usados para compreender ecossistemas biológicos. Ele ficou impressionado ao constatar que padrões rítímicos emergiam naturalmente de suas equações, tanto na química quanto na ecologia.
Por outro lado, Vito Volterra chegou às mesmas conclusões ao estudar populações de peixes no Mar Adriático. Sua pesquisa solidificou o modelo como uma ferramenta fundamental para entender relações predador-presa.
Limitações e expansões do modelo

Embora elegante, o modelo clássico de Lotka-Volterra apresenta limitações. Ele assume que:
- O alimento das presas é ilimitado.
- Os predadores dependem exclusivamente das presas para sobrevivência.
No mundo real, fatores como mudanças climáticas, doenças e adaptações evolutivas adicionam camadas de complexidade que o modelo não abrange. Por isso, cientistas frequentemente desenvolvem versões mais sofisticadas, incluindo sazonalidade e a capacidade do ambiente de suportar populações.
Impactos além da ecologia
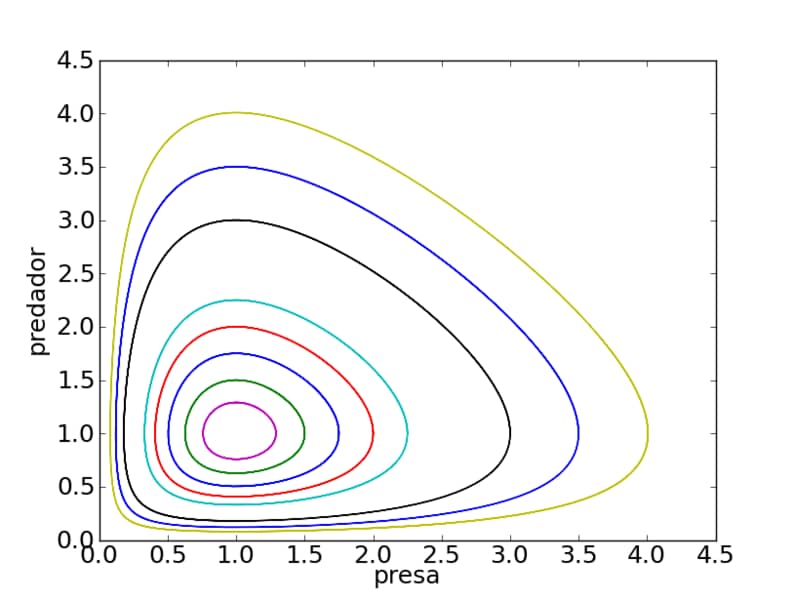
As aplicações das equações de Lotka-Volterra extrapolam os limites da biologia. Por exemplo:
- Economia: Competidores podem ser vistos como predadores e consumidores como presas.
- Marketing: Ciclos de ascensão e declínio de empresas refletem padrões semelhantes aos descritos pelo modelo.
Esse arcabouço matemático serve de base para análises em diversas áreas, provando a versatilidade e relevância das descobertas de Lotka e Volterra.
As equações de Lotka-Volterra permanecem um marco na compreensão da dinâmica ecológica, oferecendo insights valiosos que continuam a influenciar campos variados do conhecimento.


